Category: Analytic number theory

The zero-free region of the Riemann zeta function

In the previous post about the zeta function the Vinogradov–Korobov zero-free region was stated, together with what it tells us about the error term involved in using {\text{Li}(x)} to approximate {\pi(x)}. In this post it is examined how this zero-free region, together with various other zero-free regions can be derived.

The Zero-Free Regions

In the last post it was stated that it was known that only the trivial zeros of the zeta function lie outside of the strip {0 < \Re(s) < 1}. Inside this strip lie an infinite number of zeros which we refer to as the non-trivial zeros. It has been possible to produce some further restrictions on the region in which we know the non-trivial zeros lie, these results are known as the zero-free regions.

The symmetry of the location of zeros in the critical strip around both the critical line and around the real axis make it sufficient to consider zeros in the region {0.5 \leq \beta \leq 1} and {t \geq 0}. The symmetries of the zero set can then be used to derive similar results in the other three segments that the critical strip is divided into by the lines {\Re(s)=\frac{1}{2}}, and {\Im(s)=0}. For sufficiently large t the following inequalities hold for some constant c (which will be different for the different inequalities below): Continue reading →

The Riemann Zeta Function and the Prime Counting Function

This post is the first of a short miniseries looking at the distribution of prime numbers and the zeta function. The aim of this post is to motivate the link between the zeta function and the prime counting function \pi(x). It is currently planned for later posts to cover the zero-free regions and also look at generalisations of the Riemann zeta function such as Dirichlet L-functions.

The Zeta Function

For \Re(s) > 1 we define the zeta function by

{\zeta(s)=\sum_{n=1}^{\infty}n^{-s}.}

We note that by comparison with the p-series \sum_{n=1}^{\infty}n^{-p},\ p \in \mathbb{R} which is known to converge for p>1 (and diverge for 0 \leq p \leq 1), this sum converges for s in the given region.

For other values of s \neq 1 we extend the zeta function by analytic continuation. This results in a meromorphic function with a simple pole at s=1.

The Euler product formula and 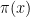\pi(x)

We will now show that for \Re(s)>1 the following identity holds:

{\sum_{n=1}^{\infty}{n^{-s}}=\prod_{p}(1-p^{-s})^{-1}.}

We can start with an intuitive heuristic justification which will then be made rigorous. Continue reading →